`: August 2020

Wednesday, August 26, 2020

PERSAMAAN KUADRAT (3)

Jumlah dan Hasil Kali Akar - akar Persamaan Kuadrat

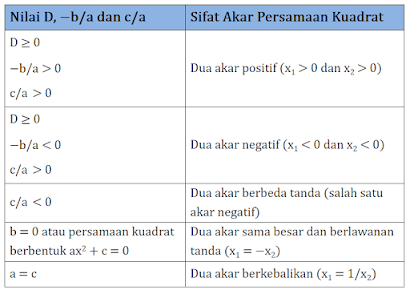
Diskriminan ( Persamaan Kuadrat)

Diskriminan yaitu suatu nilai pada persamaan (umumnya persamaan kuadrat) yang membedakan banyaknya akar persamaan itu sendiri.

Diskriminan juga memiliki arti hubungan antara koefisien dalam persamaan kuadrat untuk mencari akar persamaan dan ciri – ciri yang lainnya.

Sifat Dan Fungsi Diskriminan

Diskriminan atau bisa disebut juga Determinan merupakan suatu notasi dalam tanda akar b²-4ac yang terkadang dinotasikan dengan huruf D.

atau dapat juga dituliskan:

Contoh soal:

Gunakan sifat diskriminan untuk menganalisis akar-akar persamaan berikut ini:

Contoh lain:

Persamaan kuadrat 2x2 + 3x + 5 = 0, jika diselesaikan dengan menggunakan rumus ABC ternyata tidak mempunyai akar real atau kedua akar tidak real (imajiner). Koefisien-koefisien persamaan kuadrat 2x2 + 3x + 5 = 0 adalah a = 2, b = 3

dan c = 5, sehingga nilai diskriminannya adalah.

D = b2 – 4ac

D = (3)2 – 4(2)(5)

D = 9 – 40

D = -31

Ternyata bahwa:

D < 0, akar - akar persamaan kuadrat tersebut adalah imajiner atau tidak memiliki akar riil.

Sifat akar-akar persamaan kuadrat berdasarkan nilai diskriminan dan juga hasil penjumlahan dan perkalian akar-akarnya bisa kalian lihat dalam tabel di bawah ini.

Demikianlah paparan materi tentang cara menentukan jenis dan sifat akar-akar persamaan kuadrat dengan menggunakan nilai diskriminan lengkap dengan contoh soal dan pembahasannya. Semoga dapat bermanfaat untuk Anda. Apabila terdapat kesalahan tanda, simbol, huruf maupun angka dalam perhitungan mohon dimaklumi.

Rumus ABC

Assalamualaikum Wr. Wb

Sampai bertemu pada pembelajaran matematika

Pada kesempatan ini, ibu akan membahas materi tentang cara menetukan akar-akar persamaan kuadrat dengan menggunakan rumus ABC.

Penjelasan penggunaan rumus ABC dalam menentukan penyelesaian / akar persamaan kuadrat dapat dilihat dari video berikut ini:

Pada video tersebut disajikan bagaimana cara menyelesaikan persamaan kuadrat dengan menggunakan rumus ABC. pada prinsipnya kalian harus hafal rumusnya, dan tidak keliru pada saat menentukan nilai a, b, dan c dari persamaan kuadrat yang akan dicari penyelesaiannya.

Satu hal, kalian harus teliti dan cermat dalam melakukan perhitungan.

Paparan materi tentang penyelesaian persamaan kuadrat dengan menggunakan rumus ABC dapat kalian pelajari pada contoh soal dan pembahasan berikut ini!

Penyelesaian Persamaan Kuadrat dengan Menggunakan Rumus ABC

Demikianlah materi kali ini. semoga bermanfaat

Melengkapkan Kuadrat sempurna

Sampai jumpa di blog pembelajaran Matematikaoom

Pada postingan sebelumnya, ibu telah membahas cara menyelesaikan persamaan kuadrat dengan memfaktorkan. Selanjutnya pada kesempatan ini, kita akan belajar tentang cara menentukan akar-akar persamaan kuadrat dengan melengkapkan kuadrat sempurna.

Simak baik- baik video berikut ini:

Cara menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna:

Konsep dasar dari metode melengkapkan persamaan kuadrat sempurna adalah merubah persamaan kuadrat: ax2 + bx + c = 0.

Menggunakan dua sifat utama kuadrat sempurna: x2 + 2dx + d2 = (x+d)2 = 0 dan

x2 – 2dx + d2 =(x – d)2 = 0.

Menjadi bentuk umum melengkapkan persamaan kuadrat sempurna: (x + p)2 = q, atau (x – p)2 = q, q ≥ 0.

Langkah-langkah melengkapkan kuadrat sempurna:

$\vspace{1pc} ax^2+bx+c=0\;(\div a)\\ \vspace{1pc} \frac{a}{a}x^2+\frac{b}{a}x+\frac{c}{a}=\frac{0}{a}\\ \vspace{1pc} x^2+\frac{b}{a}x+\frac{c}{a}-\frac{c}{a}=0-\frac{c}{a}\\ \vspace{1pc} x^2+\frac{b}{a}x+(\frac{1}{2}(\frac{b}{a}))^2=-\frac{c}{a}+(\frac{1}{2}(\frac{b}{a}))^2\\ \vspace{1pc} x^2+\frac{b}{a}x+(\frac{b}{2a})^2=-\frac{c}{a}+(\frac{b}{2a})^2\\ \vspace{1pc} Misalkan\; (\frac{b}{2a})=p\\ \vspace{1pc}maka\;x^2+2px+p^2=-\frac{c}{a}+p^2\\ \vspace{1pc} Misalkan -\frac{c}{a}+p^2=q,\;maka\\ \vspace{1pc} (x+p)^2=q\\ \vspace{1pc}\sqrt{(x+p)^2}=\pm\sqrt{q}\\ \vspace{1pc}x+p=\sqrt{q}\mapsto x=-p+\sqrt{q}\\ \vspace{1pc}x+p=-\sqrt{q}\mapsto x=-p-\sqrt{q}$

Contoh 4:

Demikianlah penjelasan materi tentang cara menentukan akar-akar persamaan kuadrat dengan melengkapkan kuadrat sempurna.

Semoga Bermanfaat

Notasi Ilmiah dan Bentuk Baku

Assalamualaikum Warohmatulloohi Wabarokatu
Selamat berjumpa anak - anakku sekalian pada blog pembelajaran matematika

Semoga kalian senantiasa sehat dan menjaga kesehatan
Kita akan belajar tentang materi notasi ilmiah dan bentuk baku

Notasi Ilmiah atau bentuk baku ini digunakan untuk menuliskan bilangan yang sangat besar. atau bilangan yang sangat dekat dengan nol. Tepatnya yaitu diantara 0 dan 1 atau diantara 0 dan –1. Tujuannya yaitu agar penulisan angka tersebut lebih ringkas. Bagaimana kita mau menuliskan angka yang sangat panjang. misalnya 1230000000000 dan 0.0000000827.

Penulisan notasi ilmiah atau bentuk baku ini dilambangkan dengan a x 10ⁿ. dengan a lebih besar atau sama dengan 1 dan kurang dari 10. Dan n adalah bilangan bulat. Semua bilangan real bisa dituliskan dalam bentuk baku. Misalnya saja angka 2. Jika kita tuliskan ke dalam bentuk baku menjadi 2 x 10⁰. Karena 10⁰ = 1, maka 2 x 1 = 2.

Jika bilangan tersebut sangat besar, maka yang harus kita lakukan adalah menghitung jumlah digit pada bilangan yang sangat besar tersebut, kemudian kita kurangi 1 dan hasilnya kita tuliskan sebagai n. dan bilangan a diperoleh dari bilangan yang sangat besar tersebut kita ambil digit depannya dan kita beri koma disamping digit terdepan. Misalnya menuliskan bilangan 14240000000000000000 dalam bentuk baku.

Kita hitung jumlah digit yang ada pada bilangan tersebut. kita dapatkan ada 20 digit. Sehingga kita tuliskan n = 19. Dan a adalah angka depannya yang diberi tanda koma. Yaitu 1,424. Sehingga, bentuk bakunya kita dapatkan

14240000000000000000 = 1,424 x 10¹⁹.

Contoh yang lainnya :

87120000000 = 8,712 x 10¹⁰.

90000000000000000 = 9 x 10¹⁶.

453000000000000 = 4,53 x 10¹⁴.

536500000000000 = 5,365 x 10¹⁴.

10230000000000 = 1,023 x 10¹³.

Pertama, kita geser tanda koma tersebut ke arah kanan sampai bertemu dengan angka tak nol yang terdekat.

0,0000025 (angka semula)

00,000025 (pergeseran pertama)

000,00025 (pergeseran kedua)

0000,0025 (pergeseran ketiga)

00000,025 (pergeseran keempat)

000000,25 (pergeseran kelima)

0000002,5 (pergeseran keenam)

Sehingga didapatkan n = -6. Dan a = 2,5. Dalam bentuk baku dapat dituliskan 2,5 x 10^-6.

Contoh yang lain :

0,0301 = 3,01 x 10^-2

0,000000102 = 1,02 x 10^-7

0,009279 = 9,279x 10^-3

0,0000000000012 = 1,2 x 10^-12

Notasi pangkat ini biasanya digunakan untuk mengukur jarak-jarak pada ruang angkasa yang jaraknya sangat jauh. Atau juga digunakan dalam sebuah ukuran mikroba yang sangat kecil.

Untuk lebih jelasnya, silahkan disimak video pembelajaran berikut ini:

Sumber : Youtube https://www.youtube.com/watch?v=tKvVXc_Nka0

Demikianlah penjelasan tentang notasi ilmiah dan bentuk baku.

tetap semangat dan jaga kesehatan....

selalu cuci tangan dan menggunakan masker jika sedang keluar rumah.

Ingat selalu.......Belajar matematika itu....asyik dan menyenangkan.

Sebagai penilaian dari proses belajar kali ini, silahkan kerjakan kuis berikut,
dengan kode 3856236

KERJAKAN KUIS:

Oke anak anak sekalian, pembelajaran hari ini telah selesai.
Wassalamualaikum Wr. Wb